Description

Submit An Entry

Standings

Final Report

The Task

Given a value for n, use 3 colors to label the arcs of K_n (that is, the complete graph with n nodes) so as to minimize the number of monochromatic triangles formed.

(Definitions: A complete graph is a graph in which every pair of nodes is connected by an arc. A monochromatic triangle is a triangle whose three sides are the same color.)

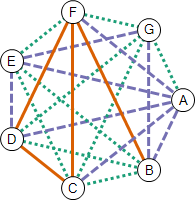
For example, here is a coloring of K₇. It contains 35 triangles, of which 3 are monochromatic (ADE, BCE and CDF). Note that this coloring does not minimize the number of monochromatic triangles – it is possible to paint the arcs of K₇ with 3 colors so that there are fewer than 3 monochromatic triangles.

The Contest

For each of the 25 values of n in {17, 23, 27, 35, 39, 47, 59, 63, 75, 83, 87, 95, 107, 123, 135, 143, 147, 159, 167, 179, 183, 195, 203, 207, 215}, submit the coloring of K_n that best minimizes the number of monochromatic triangles in the graph.

For each value of n you can submit more than one coloring, but only your best coloring will count.

See How to Enter, below, for instructions on how to submit colorings.

See The Scoring System, below, to learn how we determine the winner.

The Prizes

The participants who finish in first or second place will each receive their choice of either

• a freestanding crystal award plaque engraved with the details of their accomplishment, or
  
  
• their choice of any item from Bathsheba Sculpture worth
  • $500 or less (for the first place participant), or
  • $100 or less (for the second place participant).

How to Enter

Paste your colorings into the appropriate box on the Submit page and click Submit Entry. Format each coloring as follows:

• First, represent your coloring as an n × n matrix, with each cell (except those on the major diagonal) containing the color of the corresponding arc. Use the numbers 0, 1 and 2 to represent the three colors.
  
  
• Then, write the matrix's lower left half as a comma-delimited list of n - 1 strings. The first such string will have 1 digit and the last will have n - 1 digits. For readability, you may also place white space between the rows in addition to the comma.

For instance, the example coloring above for K₇ could be represented by the following 7×7 matrix in which 0, 1 and 2 correspond to the colors green (dotted), orange (solid) and purple (dashed), respectively.

	A	B	C	D	E	F	G
A	-	2	2	2	2	2	0
B	2	-	0	0	0	1	2
C	2	0	-	1	0	1	0
D	2	0	1	-	2	1	0
E	2	0	0	2	-	0	2
F	2	1	1	1	0	-	0
G	0	2	0	0	2	0	-

Your submission would therefore look like this:

2, 20, 201, 2002, 21110, 020020

To submit more than one coloring at a time, separate them with semicolons. Do not put a semicolon after the last coloring.

Over the course of the contest you may submit more than one coloring for the same value of n, but you should not submit a coloring unless it improves upon your previously submitted colorings. Note that your best scores can be found on the My Account page.

The Scoring System

The entrant with the highest "contest score" wins. Here's how we calculate your contest score:

• For each of the 25 values of n, we identify your best coloring. Your "raw score" for that n is the number of monochromatic triangles in the coloring.
  
  
• For each of the 25 values of n, we compute a "subscore" from 0 to 1. We do this by dividing that n's raw score into the lowest raw score for that n across all entrants.
  
  
• Your contest score is the sum of your 25 subscores.
  

If two entrants have the same contest score, we break the tie by giving preference to the entrant whose last improvement was submitted least recently.

Let's walk through a simplified example. Suppose we modify the contest by asking you to submit colorings for only three values of n: 7, 11 and 15. And further suppose that we have 3 entrants (Bonaparte, Dynamite and Solo) and that their best colorings have raw scores as follows:

	n = 7	n = 11	n = 15
Bonaparte	3	19	50
Dynamite	5	9	54
Solo	6	14	44

We note the smallest raw score for each value of n:

	n = 7	n = 11	n = 15
Smallest Raw Score	3	9	44

Finally, we compute the subscores and contest score for each entrant:

	n = 7	n = 11	n = 15	Contest Score
Bonaparte	3 / 3 = 1.000	9 / 19 = 0.474	44 / 50 = 0.880	2.354
Dynamite	3 / 5 = 0.600	9 / 9 = 1.000	44 / 54 = 0.815	2.415
Solo	3 / 6 = 0.500	9 / 14 = 0.643	44 / 44 = 1.000	2.143

Dynamite has the highest contest score and therefore wins.

Getting Your Questions Answered

First, check the FAQ section below. If you can't find the information you need there, send your question to the discussion group. If your question is of a personal nature, and not of general interest, send an email directly to Al Zimmermann.

Please note that Al Zimmermann is a cranky old man. If you send an email to Al that should have been sent to the discussion group (for example, a request for the clarification of a rule, or the report of a bug), he may ignore your email.

The Discussion Group

If you think you might enter the contest, you should join the contest discussion group . You can join either by sending a blank email to AZsPCs+subscribe@groups.io or by visiting the AZsPCs group at http://groups.io/g/AZsPCs. The discussion group serves two purposes. First, it gives contestants immediate access to important general announcements, such as rule changes or scheduled system downtime. Second, the discussion group allows contestants to interact with each other regarding programming techniques, results and anything else relevant to the contest.

Once you've joined, you can post messages by emailing your messages to AZsPCs@groups.io.

You can leave the group at any time by sending a blank email to AZsPCs+unsubscribe@groups.io.

My Lawyer Would Want Me To Say This

I reserve the right to discontinue the contest at any time. I reserve the right to disqualify any entry or entrant for any reason that suits me. I reserve the right to interpret the rules as I see fit. I reserve the right to change the contest rules in mid-contest. In all matters contest-related, my word is final.

Frequently Asked Questions

• Can teams enter the contest?

  Yes. But a team can only be formed by those who have not already entered the contest as individuals. Once you enter as an individual, team membership is no longer open to you. Likewise, once you've joined a team you can't resign from it and start submitting colorings on your own behalf.

  If you would like to form a team, please follow these instructions:

  • If they do not already exist, create individual accounts for each team member. Do not create a second account for any team member who already has one.
    
    
  • Let me know each team member's name and registered email address. It is important that no team member submit any entries to this contest until I notify you that the team has been created.
    
    
  • Unless you are satisfied with the defaults, also let me know what team name and team location you would like to use on the standings page. Note that if all team members are from the same organization, the organization name can be included in the location, e.g., "Olaf Academy, Oslo, Norway".
    – For name, the default is "{last-name-1} / {last-name-2} / ... / {last-name-n}".
    – For location, the default is the smallest geographic entity common to all team member locations.

  After I've created the team, team members can submit entries to the contest from their individual accounts. The contest engine automatically intercepts these entries and diverts them to the team account. The team is listed on the standings page.

  Note: Teams are contest-specific. Joining a team for this contest does not affect your participation in other contests.
  

• May I write a program that submits entries by bypassing my browser?

  Yes.

• May I programmatically download the standings page at regular intervals? How frequently would be reasonable?

  Yes, you may programmatically download the standings page at regular intervals. Since the standings page is cached in memory, please feel free to download it as often as once per second. If you want to download the standings page more frequently than that, please contact me first.

• What topics are appropriate for the discussion group?

  With only one exception, if it's related to AZsPCs then it's fine to talk about it in the discussion group. The exception is spoilers. Spoilers include:

  • specific colorings
  • detailed algorithms

  If you are not sure if something would be considered a spoiler, ask me.