Point Packing
| Description | Submit An Entry | Standings | Final Report |
The Point Packing Problem
Pack n distinct points in the plane as closely together as possible while satisfying the following constraints:
- Each point's coordinates are nonnegative integers.
- The distances between points are pairwise unique.
We quantify how closely together the points are packed by examining the smallest circle which can enclose them. The smaller the circle, the more closely they are considered to be packed.
Consider the following three examples for n = 4:
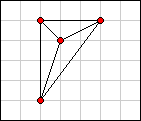 |
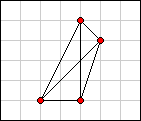 |
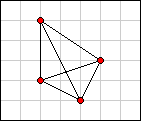 |
|
| Example A | Example B | Example C |
In examples A and B each of the six point-to-point distances is unique. Examples A and B are therefore valid packings. But in example C the distances are not unique. Example C is therefore invalid.
Now consider the smallest circles that can enclose the points in examples A and B.
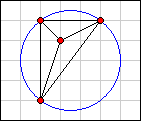 |
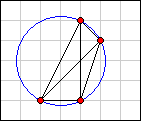 |
|
| Example A | Example B |
In example A the area of the enclosing circle is 6.25π. In example B it is 5π. Therefore, example B is the better packing.
The Contest
Submit (see How to Enter, below) your best solutions to the point packing problem for values of n from 2 to 26, inclusive. There are thus 25 individual problems which you are asked to solve.
You can submit more than one solution for the same problem, but if you do we count only your best solution. There is no penalty for submitting multiple solutions for the same problem.
See The Scoring System, below, to learn how we determine the winner.
The Prizes
First prize is your choice of any Bathsheba Grossman sculpture from one of these pages:
Second prize is your choice of any Bathsheba Grossman sculpture on one of these pages:
How to Enter
Just paste your solutions into the large box on the Submit page and click the Submit Entry button. Format your solutions as follows:
- An individual solution consists of a comma-delimited list of points.
- A point consists of a comma-delimited pair of unsigned integers, enclosed in parentheses.
- Submit multiple solutions in a single entry by separating them with semicolons. Do not put a semicolon after your last solution.
- Include spaces and line breaks anywhere you like (except within a number) to improve readability.
For example, to submit example A from above (assuming the origin
is at the lower left corner of the diagram) you might enter:
(2,1),(2,5),(3,4),(5,5)
To submit solutions for n = 4 and n = 3 in a single entry, you could
enter:
(1,0),(0,3),(3,1),(3,0);
(2,3),(0,0),(2,2)
Do not submit entries under more than one account. This is important. Do not submit entries under more than one account.
The Scoring System
We give a raw score to each solution you submit. The raw score is the area of the smallest enclosing circle divided by pi. For example, examples A and B above would receive raw scores of 6.25 and 5, respectively.
Each time you submit a solution we will merge it with your prior solutions, if any. The result will be a virtual entry containing your best solutions for each of the 25 problems. We will give each of these 25 solutions a subscore from 0 to 1 and their sum will be your contest score.
We calculate subscores for the individual solutions as follows. If your solution has the lowest raw score that was submitted for that problem, we give it 1 point; otherwise we give it only a fraction of a point. The fraction is the solution's raw score divided into the lowest raw score submitted by anyone for that same problem.
Let's walk through a simplified example. Suppose that we reduce the contest to only 3 values of n: 2, 3 and 4.
Further suppose that we have 3 entrants (Huey, Dewey and Louie) and that these are their best solutions for each of the 3 problems:
| 2 points | 3 points | 4 points | |
|---|---|---|---|
| Huey | (0,0), (1,2) | (0,2), (0,3), (3,3) | (3,1), (1,3), (3,0), (1,0) |
| Dewey | (0,1), (1,0) | (2,3), (0,0), (2,2) | (3,1), (4,2), (0,3), (4,3) |
| Louie | (0,2), (2,2) | (0,2), (2,0), (0,1) | (1,0), (0,3), (3,1), (3,0) |
The raw scores corresponding to these solutions are:
| 2 points | 3 points | 4 points | |
|---|---|---|---|
| Huey | 1.25 | 2.50 | 3.25 |
| Dewey | 0.50 | 3.25 | 4.25 |
| Louie | 1.00 | 2.00 | 4.50 |
We note the lowest raw score for each problem, as follows:
| 2 points | 3 points | 4 points | |
|---|---|---|---|
| Lowest Raw Score | 0.50 | 2.00 | 3.25 |
Finally, we compute the subscores and contest score for each entrant:
| 2 points | 3 points | 4 points | Contest Score | |
|---|---|---|---|---|
| Huey | 0.50 / 1.25 = 0.4000 | 2.00 / 2.50 = 0.8000 | 3.25 / 3.25 = 1.0000 | 2.2000 |
| Dewey | 0.50 / 0.50 = 1.0000 | 2.00 / 3.25 = 0.6154 | 3.25 / 4.25 = 0.7647 | 2.3801 |
| Louie | 0.50 / 1.00 = 0.5000 | 2.00 / 2.00 = 1.0000 | 3.25 / 4.50 = 0.7222 | 2.2222 |
Note that the scorer performs all calculations using 64-bit floating point arithmetic. In this example we truncated some results for brevity.
If two entrants have the same contest score, we break the tie by giving preference to the entrant whose last improvement was submitted least recently.
Getting Your Questions Answered
First, check the FAQ section below. If you can't find the information you need there, send your question to the discussion group. If your question is of a personal nature, and not of general interest, send an email directly to Al Zimmermann.
The Discussion Group
If you think you might enter the contest, you should join the contest discussion group. You can join either by sending a blank email here or by visiting the group on groups.io. The discussion group serves two purposes. First, it allows contestants to ask for clarifications to the rules. Be aware that sometimes these requests result in changes to the rules, and the first place those changes are announced is in the discussion group. Second, the discussion group allows contestants to interact with each other regarding programming techniques, results and anything else relevant to the contest.
My Lawyer Would Want Me To Say This
I reserve the right to discontinue the contest at any time. I reserve the right to disqualify any entry or entrant for any reason that suits me. I reserve the right to interpret the rules as I see fit. I reserve the right to change the contest rules in mid-contest. In all matters contest-related, my word is final.
Frequently Asked Questions
Can I enter the contest more than once, using different accounts?
No. Submitting entries from more than one account is not permitted.
Can teams enter the contest?
Collaboration is allowed. However, only one of the collaborators may register. If two contestants are found to have collaborated, even if this occurred before one or both registered, both will be disqualified.
What information about my solutions can I share in the discussion group?
There are two types of information that you are forbidden to post. The first is specific solutions. The second is code. You may post scores, so if you want to tell everyone that you got a raw score of 99 for n = 20 (whether true or not), go right ahead. You may also discuss the algorithms you are using.
How can I find out what my individual subscores are?
You can't. I know this is frustrating, but it's a long standing policy that isn't going to change. Over the years it's been hotly debated in the discussion group and the contest administrator appears to have very strong feelings on the matter. You're going to have to learn to live with it. And I'd think twice before raising the issue yet again.
After I submit a solution, the scorer shows me the solution's "canonical representation". What is that?
After the scorer calculates your raw score it rotates, reflects, relocates and/or re-orders the points in your solution to create a standard representation of it. If you plot the points of the canonical solution, you'll see that it is equivalent to your original solution. Having canonical versions of your solutions makes it easier to notice when two seemingly different solutions are fundamentally the same.