The Task
Given a positive integer
n,
create a polygon by selecting
n
vertices from an
n × n
grid of points, subject to the following constraints:
-
No two vertices are from the same row or from the same column of the grid.
-
No two sides have the same slope.
-
No two sides intersect, except at a shared vertex.
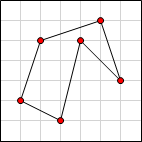
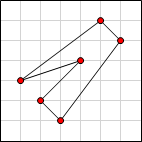
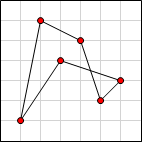
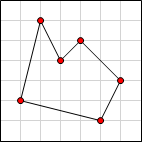
Here are some examples for n = 6:
 |
 |
 |
 |
Example 1
Invalid. Two vertices
from the same row. |
Example 2
Invalid. Two sides have
the same slope. |
Example 3
Invalid. Sides intersect. |
Example 4
Valid. |
A Word From Our Sponsor
The Contest
For each integer
n
from the list below submit two polygons as described above.
One of the polygons should have the largest area you can create;
the other should have the smallest.
See How to Enter,
below, for instructions on how to submit your polygons.
The values of n are
5, 7, 11, 17, 23, 29, 37, 47, 59, 71, 83, 97, 113, 131,
149, 167, 191, 223, 257, 293, 331, 373, 419, 467, 521.
For each value of
n
you can submit more than two polygons if you wish,
but only the most extreme
– that is, the one with the largest area and the one with the smallest –
will count.
See The Scoring System, below, to
learn how we determine the winner.
This contest was inspired by Cihan Altay's 2002 Loop Pool puzzle.
The Prizes
First prize: Any item, up to a $500 value, from Bathsheba Sculpture.
Second prize: Any item, up to a $100 value, from the same site.
Al Zimmermann is particularly partial to the metal sculptures,
but if you win don't let that influence your choice –
the laser crystals are also pretty cool.
How to Enter
Just paste your polygons into the large box on the
Submit page and click the Submit
Entry button. Format your polygons as follows:
-
An individual polygon consists of a comma-delimited list of points.
-
Each point consists of an x-coordinate and a y-coordinate,
separated by a comma and enclosed in parentheses.
Coordinates must range from 1 to
n.
-
To submit more than one polygon at a time,
separate them with semicolons.
Do not put a semicolon after your last polygon.
-
Include spaces and line breaks anywhere you like (except within a
number) to improve readability.
For example,
you could submit the polygon from Example 4 above by entering:
(1,2), (2,6), (3,4), (4,5), (6,3), (5,1)
The Scoring System
The entrant with the highest contest score wins.
Here's how we calculate your contest score:
-
For each of the 25 possible values of n, we
identify the polygon you submitted with the
largest area and the one with
the smallest. The difference between these
two areas is your raw score for
that n.
-
For each of the 25 possible values of n, we
also identify the polygon with the largest area
submitted by any entrant and the polygon with
the smallest area submitted by any entrant.
The difference between those two numbers is
the conjectural best for that n.
-
Then, for each n, we calculate your subscore
for that n by dividing your raw score by the
conjectural best.
-
Finally, we calculate your contest score by
adding up your 25 subscores.
If two entrants have the same contest score, we break
the tie by giving preference to the entrant whose last
improvement was submitted least recently.
Let's walk through a simplified example. Suppose that we modify
the contest by asking you to submit polygons for only three values of n: 6, 8 and 10.
Further suppose that we have 3 entrants (Hillary,
Donald and Gary) and that these are their most
extreme polygons and their raw scores:
|
n = 6 |
n = 8 |
n = 10 |
| Min Area | Max Area | Raw
Score |
Min Area | Max Area | Raw
Score |
Min Area | Max Area | Raw
Score |
| Hillary |
6.5 | 13.5 | 7.0 |
14.5 | 23.5 | 9.0 |
24.5 | 34.5 | 10.0 |
| Donald |
5.5 | 11.0 | 5.5 |
7.0 | 18.5 | 11.5 |
28.0 | 40.5 | 12.5 |
| Gary |
9.0 | 9.5 | 0.5 |
15.5 | 17.0 | 1.5 |
32.0 | 33.5 | 1.5 |
We note the conjectural best for each problem, as follows:
|
n = 6 |
n = 8 |
n = 10 |
| Min Area | Max Area | Conjectural
Best |
Min Area | Max Area | Conjectural
Best |
Min Area | Max Area | Conjectural
Best |
| All Entrants |
5.5 | 13.5 | 8.0 |
7.0 | 23.5 | 16.5 |
24.5 | 40.5 | 16.0 |
Finally, we compute the subscores and contest score for each entrant:
|
n = 6 |
n = 8 |
n = 10 |
Contest Score |
| Hillary |
7.0 / 8.0 = 0.8750 |
9.0 / 16.5 = 0.5455 |
10.0 / 16.0 = 0.6250 |
2.0455 |
| Donald |
5.5 / 8.0 = 0.6875 |
11.5 / 16.5 = 0.6970 |
12.5 / 16.0 = 0.7813 |
2.1657 |
| Gary |
0.5 / 8.0 = 0.0625 |
1.5 / 16.5 = 0.0909 |
1.5 / 16.0 = 0.0938 |
0.2472 |
Donald has the highest contest score and therefore wins.
Getting Your Questions Answered
First, check the FAQ section below. If you can't
find the information you need there, send your question to the
discussion group.
If your question is of a personal nature, and not
of general interest, send an email directly to
Al Zimmermann.
The Discussion Group
If you think you might enter the contest, you should join the
contest discussion group. You can join either by sending a blank email
here or by visiting the group on
groups.io.
The discussion group serves two purposes. First,
it allows contestants to ask for clarifications to the rules. Be aware that
sometimes these requests result in changes to the rules, and the first place
those changes are announced is in the discussion group. Second, the discussion
group allows contestants to interact with each other regarding programming
techniques, results and anything else relevant to the contest.
My Lawyer Would Want Me To Say This
I reserve the right to discontinue the contest at any time. I reserve the right
to disqualify any entry or entrant for any reason that suits me. I reserve the
right to interpret the rules as I see fit. I reserve the right to change the
contest rules in mid-contest. In all matters contest-related, my word is final.
Frequently Asked Questions
-
Can teams enter the contest?
Yes. But a team can only be formed by those who have not
already entered the contest as individuals. Once you enter
as an individual, team membership is no longer open to you.
Likewise, once you've joined a team you can't break away and
start submitting solutions on your own behalf.
If you would like to form a team, please follow these instructions:
-
If they do not already exist, create individual accounts for each team member.
Do not create a second account for any team member who already has one.
-
Let me know
each team member's registered email address. It is important that
no team member submit any entries to this contest until I notify you
that the team has been created and that it is okay to begin submitting.
-
After I've created the team, team members can submit entries to
the contest from their individual accounts. The contest engine automatically
intercepts these entries and diverts them to the team account. The team is
listed on the standings page.
-
Note: Teams are contest-specific. Joining a team for this
contest does not affect your participation in other contests.
-
Can I write a program that submits entries by bypassing my browser?
Yes and no. If your program keeps track of your submissions
and only submits improved solutions, yes. Otherwise, no. For
the Son of Darts contest a few years ago, there was one participant
who wrote a program to exhaustively generate all possible solutions
and submit every one of them. Within two weeks he'd submitted over
a million entries. The AZsPCs database had grown to 10 times its
normal size and this individual was single-handedly responsible for 90%
of the entries in the database. Please compute responsibly.
-
What topics are appropriate for the discussion group?
With only one exception, if it's related to AZsPCs then
it's fine to talk about it in the discussion group. The
exception is spoilers. Spoilers include:
- specific solutions
- detailed algorithms
If you are not sure if something would be considered a spoiler,
ask me.
-
After I submit a solution, the scorer shows me the
solution's "canonical representation". What is that?
After the scorer calculates your raw score it may rotate and
reflect your polygon, reverse the order of its points, and/or
choose a different starting point in order to create a standard
(or "canonical") representation. Representing solutions
canonically makes it easier to notice when two seemingly
different solutions are fundamentally the same.
-
My cousin, who was 1st runner-up in last year's Miss Parador
contest, would like to know if you are married. Are you?
Please ask her to email me privately.
|



